Investigating Terrorist and Smuggling Games

Dr. Jim Taylor, Naval Postgraduate School

Download PowerPoint Presentation

Game Theory involves reducing uncertainty in order to improve decision-making. In two archetype situations Game Theory does not apply to military decision-making. There may be limitations in applying Game Theory to the terrorist game, just as one has to be careful in applying Game Theory to command decision-making.

Dr. Taylor emphasizes: “You have to think of the theory for simple and complex situations and look at this in terms of reducing to a certainty what an opponent will do.”

See enlargement

The terrorist game, in its simplest version, shows two locations, denoted as L1 and L2, that the terrorist can attack in any given time period. The counter-terrorist (or Defender) will not know where the attack will occur, and has only enough resources to defend one location. This defense can be done openly (interpreted as a pure strategy defense) or it can be done in complete security (which is interpreted as a mixed strategy defense). The terrorist can act similarly.

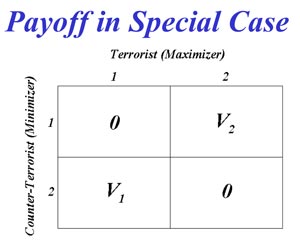
In the development of the payoff matrix, the counter-terrorist can attack the terrorist in a number of options with the payoff being:

1. Success in capture of the terrorist,
2. The terrorist blowing himself up, or
3. The counter-terrorist can be captured or destroyed himself.

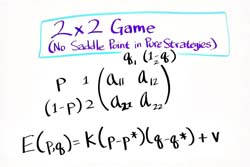The counter-terrorist wants to minimize his loss. However, low value targets can be compromised. If the terrorist attacks L1, which the counter-terrorist has defended, the attack fails and the terrorist will gain nothing or only a small negative value.

So, Dr. Taylor asks how do we identify an optimal course of action? He proposes that we want to “blow away the fog of decision-making.” It becomes a silent bidding war where one may announce his intentions and the other side reacts. Strategies may also arise as one of the decision-makers dominates, leaving no choice left for the opposition.

In the 2x2 game there are no “saddle points” in pure strategies:

If you don't have a good security system the terrorist will get through to your highly valued target. The question comes up of whether there is a threshold for the target value. P1 is the probability that the Defender captures the terrorist. T1 is the more valuable target.

In the smuggling game, you have different routes and borders to be guarded. The smuggler seeks to maximize the value of what gets through. It is always better for the counter-smuggler to guard the higher probability-of-intercept location less, because the smuggler will most likely avoid it. The smuggler will concentrate on moving in areas where there will be a lower probability of intercept.

Game Theory provides structure and enables one to think like the opponent. But the results don't repeat themselves because everything will be thought as they are re-enacted. Insights will be given, but we need to be aware that there is a difference between the smuggler and the terrorist.

For what it's worth in talking about evasion games, Washburn was not aware of Breakwell, who discovered a strategy called the Swerve. Dr. Taylor highly recommends looking into what Breakwell did.

Jim reminded us that the perceived extreme irrationality of the terrorist can still be highly predictable. What is culturally irrational may still be predictable in terms of behavior and one can still anticipate. Once you get to a case where there is no saddle point, what is critical is the chosen archetype or paradigm. It is this choice of thought systems that determine the solution set.

Consider what Game Theory has to offer to come to new conclusions and get rid of the uncertainty. One has to determine whether a model produces patterns that may and do occur in the real world.

The adversary thinks in terms of the long run, and this may help to make him more predictable. Sometimes, in acting against an adversary, one can't afford to act predictably.