Another View of Small World

Brian McCue, Center for Naval Analyses

Download Presentation

This afternoon I am going to take a look at "The Small World Networks" in a little different way than other literature has done. The giant sized footprints of Duncan Watts and Peter Dodds notwithstanding, I have found a different way of looking at small worlds, that is quite consistent with the aphorisms we use.

Click image for enlargement

When someone pops up that you've been introduced to before, you say, "It's a small world".

When we meet someone in an unexpected contex, there is an element of coincidence there. For example, if we meet a lieutenant at the SSG among all these colonels and captains. And then he pops up at a MORS meeting, you aren't that surprised, because he must be a smart guy. Anyhow, that's how I met Jeff Cares. I didn't say "It's a small world."

I did say this when I had a job interview and a few hours later, I witnessed a car accident. I pulled over to be a witness to the incident and out pops the person I just had an interview with... now THAT's when you say, "It's a small world!"

(I did get the job, by the way.)

The small world literature largely addresses:

• Lengths of typical acquaintance chains (ex. the Kevin Bacon game, “six degrees of separation” joining individuals, etc.).
• Sizes of typical acquaintance volumes (numbers of people known to an individual.)
• Network structures of individuals’ acquaintanceships.

It is hard for people to determine how many people they know. How do you define "know"? Is it that you know their name, or know them well enough to call them by their first name, or that you can touch them? It is hard to estimate how many people people know. People may know someone enough to recognize them when they walk through the door.

When we say, "It's a small world," are we talking about acquaintance chain, acquaintance volume or are we saying something about structures?

Now if we meet someone at a meeting, for example a woman whom we met at church. Would we say, "It's a small acquaintance chain"? No. Duh!

Would we, in the same circumstance blurt out, "It's a small acquaintance volume?" Definitely not a good pick up line. Because that would mean we don't know very many people. That's not what we are expressing when we meet someone in an unexpected context.

What we are saying is that it is a small world, because I keep sampling it, at not a great rate, but I keep getting these "repeats".

When we meet someone we are "pulling a ball out of an urn". And we keep getting the same ones. That must mean that there are not that many balls in the urn. It must be a small world because I sample the world, at not great rate, and keep getting repeats. The "small world"--or the operational world--is the world from which we would be sampling, if we were sampling randomly from a structuraless world. And the fact that the virtual, operational world is "small" is a statement about the "real world".

The factors are:

1. Length of the Chain: How many steps are you from the other person?

2. Volume: How many people do you know?

In regards to Kevin Bacon, he has a large acquaintance volume, because of the numbers of films and diversity of films he has made. He is probably connected by short chains, to you, because of the volume, but that assumes something about sampling.

The small world that I am talking about has a very large estimate of people, but not an infinite number, from which I'm sampling, and getting these repeats. If I sampled without structure, if I were truly sampling the world at random, how big would it be to get me the level of repeats that I'm getting?

In fact, I sample in a very structured way:

1. I live in North America
2. I work with academic type people (most of whom don't see movies)

Of the six billion people in the world, there are just people whom I'm not going to meet! But there is a size that the world could be, if I were sampling it randomly, and get the number of repeats that I'm getting.

I suppose I should mention the town of Maybury.

So, the evocation of this imaginary, structuraless world, is a statement about the real, large, structured world.

If you actually got the size of the world, and it turned out to be... 600. That doesn't say that you know 600 people, but you are sampling in such a way that you may not even meet all the people in that world, for example you live in a monastery and only interact with a few individuals.

When we say that it's "plane sailing" it means that you can pretend the world is flat. Now does the navigator think that the world is really flat? No. Does he say the world is flatter that the last time he traveled across it? No.

He is saying this, because he is close enough to his destination to act as if it were so. His fictitious statement that the world is flat, however, is a statement that reflects the real situation.

The sample that we are pulling from is a condition of probability (ex. a person working in their profession will meet more random people and repeats within their profession. The personal condition determines the "urn" from which we can draw samples.

Estimating the Operational World

The evocation of this imaginary, small, structureless world is a statement about the structure of the real, large, structured world.

We will estimate the size of this "operational world" and thereby learn about the real world.

The math starts here (for accurate representations of formulas, download presentation:

• W = size of an individual's "world" (Does not include individual herself.)
• I = Number of meetings she has had
• Ik= number of meetings of person k (Ik is defined for k = 1, 2, W)
• Wj = number of individuals met j times (Wj is defined for j = 0, 1, 2,...I )

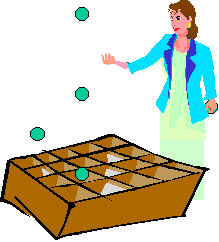Dropping I balls over W boxes

1. W I ways do to it.
2. We don't care about the order of introductions.
3. We don't care which person is which.

A box with two balls is a coincidental re-introduction.We are dropping balls (which are introductions) to boxes (that are people).

Small Village Sample

A vistitor meets randomly 9 people, two of them twice, given the total popluation of W, the probabilty of this happening is 24 people are probably in the village.

Now we are going to try to get real. W1 the number of people that we have met one time and I1.

We can not ask you how many people there are in the world.

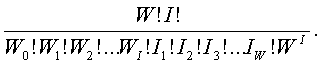
Likelihood, A Function of W

Probability, given W, that what happened would happen. Can be used to estimate W. Suggests that there are about 24 people.

Realistic Numbers

W1 and I1 are nearly equal to I These equal a few thousand for most people, but can only be estimated approximately. For j,k > 1,Wj and Ik are small and people might recall them.

More Definitions

The number of surprise introductions are remembered because they do not occur that often.

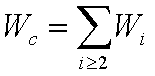
How do you estimate I?

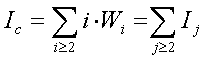
S = Ic - Wc

S is the number of surprising reintroductions.

Likelihood of W, re-written

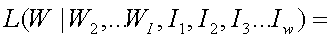
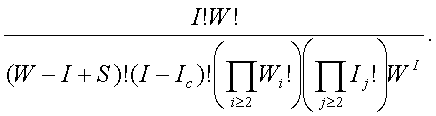
With the first part of the answer being things a person might remember. What the person doesn't remember has factorial = 1 so it doesn't matter.

Maximizing L(W)

L(W) still contains factorials of some big numbers. But we can find the W that maximizes by finding W such that...

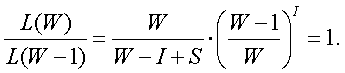
Estimating I

The phonebook test of Freeman and Thompson presents 301 surnames and asks the subject how many are names of people she knows.

I = score x total names in book/301. Book contains about 100,000 names. Typical result is 1,000 - 6,000.

Estimating W

A person has I = 2000, S = 1: this leads to a W of about 2,000,000 in: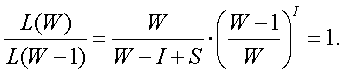

If I = 4,320 and S = 12, W = 775,000

But it's worth computing L(W)

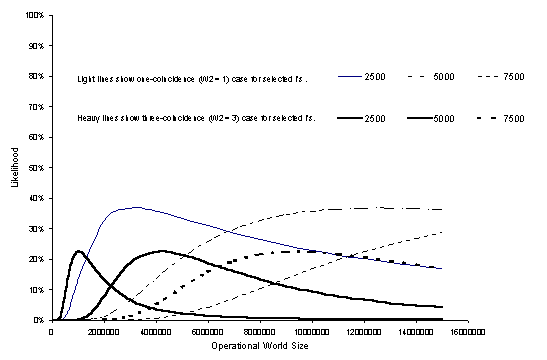
Observations on likelihoods

Maxima are surprisingly high. Even S = 3 is enough to make a distinct peak. Resulting world sizes are:

• Much less than the real world's size.
• Comparable to (mostly less than or equal to) city sizes.

Conclusions

We each might as well be drawing a lifetime's introductions from a small city.

For people who really do draw introductions from limited populations, coincidental re-introductions could be used to estimate I.

Discussion

But what about those acquaintance chains, and the six degrees of separation? In light of US population size and estimates of I, six degrees is surprisingly many, not surprisingly few. For a random structure, four degrees would be plenty. Small world-size suggests that extra degrees are needed to make jumps from world to world.

What about the six degrees of freedom? What about the introductions? If you know at least 1000 poeople, you should be able to get to everyone in the US. You need the extra steps to be able to get from one cluster to the next.

Future work

1. Get solid work on conicidental re-introductions
2. Do math to find: why
3. Think about how small worlds might connect and how we could, perhaps, through coincidental reintroductions, discover how they really do connect.

Questions

Military Applications: This paper grew out of U-boat war. How many enemy transfer records have we not heard. How many have we not detected.

Milgram decided that we were connected by chains that were very short. Tracked things and got an average of six with a package that might get to a particular person who knows.

Partial Bibliography

Manfred Kochen (editor), 1989, The Small World, Ablex Publishing Corporation, Norwood, MA. Includes the following chapters: H. Russell Bernard, Eugene C. Johnsen, Peter D. Killworth, Scott Robinson, “Estimating the Size of an Average Personal Network and of an Event Subpopulation.”

Linton C. Freeman and Claire R. Thompson, “Estimating Acquaintanceship Volume.”
Alden S. Klovdahl, “Urban Social Networks, Some Methodological Problems and Possibilities”

Ithiel de Sola Pool and Manfred Kochen, “Contacts and Influence,” originally published in Social Networks 1 (1978), pages 5-51.

Brian McCue, “Estimating the Number of Unheard U-boats: A Problem in Traffic Analysis,” 2000, Military Operations Research, Volume 5, Number 4, pp 5-18.
Stanley Milgram, “The Small World Problem,” 1967 Psychology Today 1, pp 61-67.

Ray Solomonoff and Anatol Rapaport, 1951, “Connectivity of Random Nets,” Bulletin of Mathematical Biophysics 13, pp 107-117.

Ray Solomonoff, 1952, “An Exact Method for the Computation of the Connectivity of Random Nets,” Bulletin of Mathematical Biophysics 14, pp 153-157.

Jeffrey Travers and Stanley Milgram, 1970, “An experimental study of the small world problem, “ Sociometry 32, pp. 425-443.

Duncan Watts, 1999, Small Worlds: The Dynamics of Networks between Order and Randomness, Princeton, Princeton University Press.